Barisan Cauchy

Pada artikel barisan konvergen, telah dijelaskan bagaimana definisi suatu barisan konvergen. Permasalahan yang sering ditemui pada barisan konvergen adalah menentukan limit barisannya. Pada sistem bilangan real, barisan Cauchy menjadi salah satu alternatif untuk menyimpulkan kekonvergenan suatu barisan, tanpa perlu mencari limit barisannya. Barisan Cauchy diperkenalkan oleh seorang matematikawan Perancis bernama Augustin-Louis Cauchy. Secara geometris, pada barisan Cauchy ditandai dengan jarak di antara suku-sukunya semakin lama semakin mengecil. Hal tersebut dituangkan dalam definisinya sebagai berikut.

Definisi Barisan Cauchy

Barisan bilangan real $(x_n)$ disebut barisan Cauchy jika untuk setiap $\epsilon >0$ , ada $n_0 \in \mathbb{N}$ sedemikian sehingga untuk setiap $n,m \geq n_0$ berlaku $|x_n-x_m|<\epsilon.$

Contoh-contoh Barisan Cauchy.
1. Barisan $\left(\displaystyle \frac{1}{n}\right)$ merupakan barisan Cauchy.

Bukti: Diambil sebarang $\epsilon>0.$ Menurut sifat Archimedes, ada $n_0 \in \mathbb{N}$ sedemikian sehingga $\displaystyle \frac {1}{n_0}<\displaystyle \frac {\epsilon}{2}$ .
Jadi, untuk setiap $m,n \in \mathbb{N}$ dengan $m,n \geq n_0$ berlaku

$|x_n-x_m|=\left|\displaystyle \frac{1}{n}-\displaystyle \frac{1}{m}\right|\leq \left|\displaystyle \frac{1}{n}\right|+\left|\displaystyle \frac{1}{m}\right|\leq \displaystyle \frac {1}{n_0}+\displaystyle \frac {1}{n_0}<\displaystyle \frac {\epsilon}{2}+\displaystyle \frac {\epsilon}{2}=\epsilon.$

2. Barisan $\left(\displaystyle \frac{1}{n^2}\right)$ merupakan barisan Cauchy.

3. Barisan $\left(\displaystyle \frac{n+1}{n}\right)$ merupakan barisan Cauchy.

Berikut dijelaskan bagaimana hubungan antara barisan Cauchy dan barisan terbatas.

Teorema

Diketahui $(x_n)$ barisan bilangan real. Jika $(x_n)$ barisan Cauchy, maka $(x_n)$ terbatas.

Bukti:
Diketahui $(x_n)$ barisan Cauchy. Diambil $\epsilon=1$ , maka terdapat $n_0 \in \mathbb{N}$ sehingga untuk setiap $n,m \geq n_0$ berlaku $|x_n-x_m|<1.$
Jadi, untuk setiap $n \geq n_0$ berlaku $|x_n-x_{n_0}|<1$ yang berakibat $|x_n|<|x_{n_0}|+1.$
Diambil $M=\max \{|x_1|,|x_2|,...,|x_{n_0-1}|,1+|x_{n_0}|\}$ , maka $|x_n|\leq M$ , untuk setiap $n \in \mathbb{N}$ .
Dengan kata lain, $(x_n)$ terbatas.

Hubungan antara barisan Cauchy dan barisan terbatas selanjutnya akan digunakan pada pembuktian hubungan antara barisan konvergen dan barisan Cauchy yang akan dijelaskan pada teorema berikut.

Teorema

Diberikan barisan bilangan real $(x_n)$ . Barisan $(x_n)$ konvergen jika dan hanya jika $(x_n)$ merupakan barisan Cauchy.

Bukti: $(\Rightarrow)$
Diambil sembarang $\epsilon >0$ . Karena $(x_n)$ konvergen, misalkan ke $x \in \mathbb{R}$ , maka ada $n_0 \in \mathbb{N}$ sedemikian sehingga untuk setiap $n \geq n_0$ berlaku $|x_n-x|<\frac {\epsilon}{2}.$ Jadi, untuk setiap $n,m \geq n_0$ akan berlaku:

$\begin{equation*} \begin{split} |x_n-x_m|&=|x_n-x+x-x_m|\\ &\leq |x_n-x|+|x-x_m|\\ & < \frac {\epsilon}{2}+\frac {\epsilon}{2}\\ & = \epsilon. \end{split} \end{equation*}$

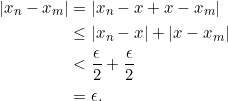
Dengan kata lain, $(x_n)$ merupakan barisan Cauchy.

$(\Leftarrow)$

Diketahui $(x_n)$ barisan Cauchy.Diambil $\epsilon >0$ , maka terdapat $n_0 \in \mathbb{N}$ sehingga untuk setiap $n,m \geq n_0$ berlaku

$|x_n-x_m|<\frac {\epsilon}{2}.$

Karena $(x_n)$ barisan Cauchy, maka $(x_n)$ terbatas sehingga $(x_n)$ memuat barisan bagian $(x_{n_k})$ yang konvergen, misalkan ke $x'$ .
Oleh karena itu, ada $k \geq n_0$ dengan $k \in \{n_1,n_2,...\}$ sedemikian sehingga

$|x_k-x'|<\frac {\epsilon}{2}.$

Akibatnya, untuk $m=k$ berlaku

$\begin{equation*} \begin{split} |x_n-x'|&=|x_n-x_k+x_k-x'|\\ &\leq |x_n-x_k|+|x_k-x'|\\ & < \frac {\epsilon}{2}+\frac {\epsilon}{2}\\ & = \epsilon. \end{split} \end{equation*}$

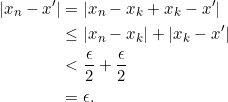
Jadi, terbukti barisan $(x_n)$ konvergen ke $x'$ .

Adanya ekuivalensi antara barisan Cauchy dan barisan konvergen di $\mathbb{R}$ , seperti yang sudah dijelaskan di Teorema di atas, menjadi sifat utama untuk pembuktian barisan konvergen, tanpa melalui limit barisannya. Karena barisan Cauchy secara definisi menggunakan konsep jarak (metric), selanjutnya konsep jarak tersebut digeneralisasi untuk sebarang ruang metrik. Barisan Cauchy dan barisan konvergen menjadi sifat yang sangat penting dalam penentuan kelengkapan suatu ruang metrik.

Mari Belajar Bersama Kami!

Barisan Cauchy

Definisi Barisan Cauchy

Teorema

Teorema

Mari Belajar Bersama Kami!

Submit a Comment Cancel reply