Deret Konvergen
Pada artikel barisan konvergen, telah dijelaskan bagaimana definisi suatu barisan konvergen. Sebagaimana kita ketahui, deret merupakan jumlahan suku-suku suatu barisan. Dalam artikel ini, akan dijelaskan bagaimana kekonvergenan suatu deret. Deret yang konvergen sangat ditentukan oleh bagaimana kekonvergenan barisan jumlah parsialnya.
Definisi Deret Konvergen
Deret ![]() dikatakan konvergen jika barisan jumlah parsial
dikatakan konvergen jika barisan jumlah parsial ![]() konvergen.
konvergen.
Dengan kata lain, jika ![]() , maka
, maka
![]()
Deret ![]() dikatakan divergen jika barisan
dikatakan divergen jika barisan ![]() divergen.
divergen.
Untuk lebih memperjelas definisi deret konvergen di atas, berikut diberikan salah satu contoh deret konvergen.
Deret ![]() merupakan deret konvergen. Berikut pembuktiannya.
merupakan deret konvergen. Berikut pembuktiannya.
Perhatikan deret deret ![]() dengan
dengan ![]() .
.
Selanjutnya,
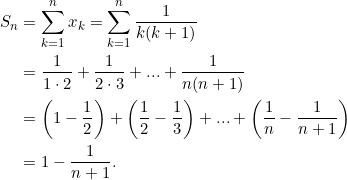
Jadi, ![]() Dengan kata lain,deret
Dengan kata lain,deret ![]() konvergen.
konvergen.
Contoh deret konvergen lainnya adalah deret geometri. Misalkan diketahui barisan ![]() . Deret
. Deret ![]() konvergen ke
konvergen ke ![]() , jika
, jika ![]() Berikut pembuktiannya.
Berikut pembuktiannya.
Tuliskan
![]()
maka
![]()
Karena ![]() , maka
, maka ![]() , sehingga
, sehingga
![]()
atau
![]()
atau
![]()
Dengan kata lain, deret ![]() konvergen ke
konvergen ke ![]() .
.
Salah satu sifat yang cukup penting pada deret konvergen adalah bagaimana kekonvergenan suatu deret mengakibatkan nilai limit dari barisannya menjadi nol. Sifat tersebut akan dijelaskan pada teorema berikut.
Teorema
Jika ![]() konvergen, maka
konvergen, maka ![]()
Berikut pembuktian Teorema di atas.
Diperhatikan bahwa, ![]() dan
dan ![]() sehingga
sehingga ![]()
Diketahui ![]() konvergen, katakan ke
konvergen, katakan ke ![]() . Berarti
. Berarti ![]() .
.
Akibatnya, ![]() .
.
Jadi,
![]() .
.
Suatu deret yang divergen, selain bisa ditunjukkan menggunakan barisan jumlah parsialnya yang divergen, sebagai alternatif pembuktian yang lain bisa menggunakan kontraposisi dari Teorema di atas, yaitu
Jika ![]() , maka
, maka ![]() divergen.
divergen.
Sifat tersebut relatif lebih mudah untuk digunakan dalam hal pembuktian deret konvergen, tanpa melalui limit barisan jumlah parsialnya.
Sifat sebaliknya dari Teorema di atas, belum tentu berlaku, yaitu
Jika ![]() , maka
, maka ![]() belum tentu konvergen.
belum tentu konvergen.
Sebagai contoh deret harmonik ![]() divergen, walaupun
divergen, walaupun ![]()

Materi tentang deret konver gen ka