Ruang Metrik

Ruang metrik adalah himpunan yang memiliki definisi jarak antara elemen. Metrik pada X adalah sebuah fungsi yang didefinisikan pada X yang mendefinisikan jarak antara dua titik pada X. Ruang metrik merupakan salah satu konsep yang penting dalam bidang analisis. Hal ini dikarenakan konsep ruang metrik banyak digunakan dalam pembahasan konsep-konsep analisis yang lain dan juga digunakan di bidang aplikasi. Sebagai contoh, pembahasan konsep limit pada himpunan bilangan real menggunakan nilai mutlak |x–y| untuk menyatakan jarak antara titik x dan y. Peranan nilai mutlak ini dapat diperluas dengan metrik.

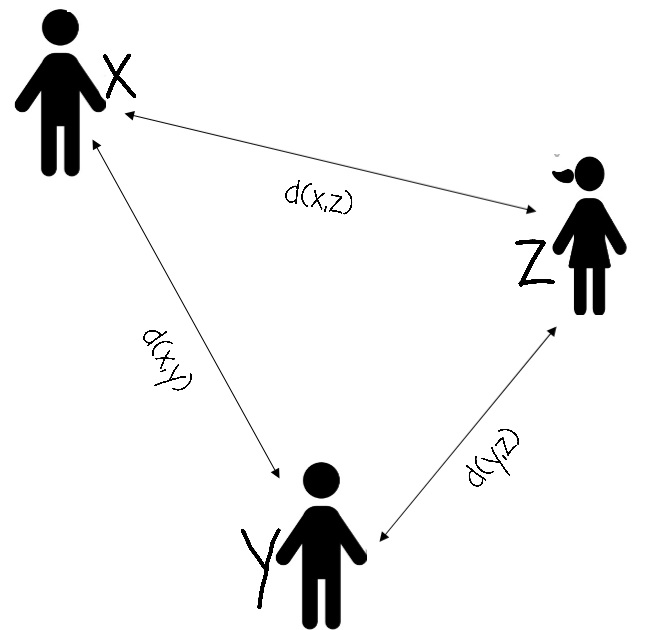
Definisi Metrik

Diberikan sebarang himpunan tak kosong $X$ . Fungsi $d:\; X\;\times\; X\rightarrow\mathbb{R}$ yang memenuhi sifat-sifat
(M1) $d(x,y)\geq 0$ untuk setiap $x,y\in X$
(M2) $d(x,y)=0$ jika dan hanya jika $x=y \text{ (definit positif) }$
(M3) $d(x,y)=d(y,x)$ untuk setiap $x,y\in X \text{ (simetris) }$
(M4) $d(x,y)\leq d(x,z)+d(y,z)$ untuk setiap $x,y,z\in X \text{ (Ketaksamaan segitiga) }$
disebut jarak (metrik) pada $X$ . Pasangan $(X,d)$ disebut dengan ruang metrik.

Contoh 1:

Didefinisikan fungsi $d_1 : \mathbb{R}\times\mathbb{R} \rightarrow \mathbb{R}$ dengan

$d_1(x,y)=|x-y| \text{ untuk setiap } x, y \in \mathbb{R}.$

Sifat $(1)-(4)$ dipenuhi dari sifat nilai mutlak (sifat-sifat nilai mutlak dapat dilihat di sini). Selanjutnya, metrik $d_1$ dikenal dengan metrik biasa.

Diberikan ruang metrik $(X,d)$ dan sebarang titik $a\in X$ dan konstanta real $r>0$ , didefinisikan himpunan:

$N_{r}(a)=\{x\in X:\; d(x,a)<r\}$

yang disebut dengan persekitaran titik $a$ dengan jari-jari $r$ . Dari himpunan tersebut, sifat-sifat topologis dari ruang metrik dapat ditelusuri lebih lanjut.
Khusus untuk ruang metrik $(\mathbb{R}, d)$ dengan metrik biasa, maka diperoleh sifat-sifat topologis yang berada di Dasar-dasar topologi.

Contoh 2:

Berikut diberikan contoh metrik pada $\mathbb{R}^2$ .

1. Fungsi jarak berikut diperoleh dari Teorema Phytagoras yang didefinisikan pada $\mathbb{R}^2$ . Didefinisikan metrik $d_2 : \mathbb{R}^2\times\mathbb{R}^2 \rightarrow \mathbb{R}$ dengan

$d_2(\bar{x},\bar{y})=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2} \text{ untuk setiap } \bar{x},\bar{y} \in \mathbb{R}^2$

dengan $\bar{x}=(x_1, x_2), \bar{y}=(y_1, y_2)$ . Selanjutnya, metrik $d_2$ dikenal dengan metrik Euclid.

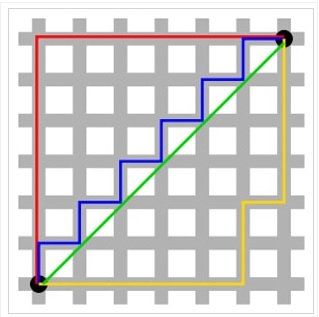
2. Fungsi jarak berikut dikenal dengan taxi cab metrik. Didefinisikan metrik $d_3 : \mathbb{R}^2\times\mathbb{R}^2 \rightarrow \mathbb{R}$ dengan

$d_3(\bar{x},\bar{y})=|x_1-y_1|+|x_2-y_2| \text{ untuk setiap } \bar{x}=(x_1, x_2), \bar{y}=(y_1, y_2) \in \mathbb{R}^2.$

Sifat (1)-(3) dipenuhi dari sifat nilai mutlak. Sifat ketaksamaan segitiga dipenuhi karena untuk setiap $\bar{x}, \bar{y}, \bar{z} \in \mathbb{R}^2$

$\begin{array}{ll} d_3(\bar{x}, \bar{y}) & =|x_1-y_1|+|x_2-y_2|\\ & = |x_1-z_1+z_1-y_1|+|x_2-z_2+z_2 -y_2|\\ & \leq |x_1-z_1|+|z_1-y_1| + |x_2-z_2|+|z_2 -y_2|\\ & = d(\bar{x}, \bar{z})+d(\bar{y}, \bar{z}). \end{array}$

Contoh 3:

Diketahui sebarang himpunan tak kosong $X$ . Fungsi $d_4: X \times X \rightarrow \mathbb{R}$ merupakan metrik dengan

$d_4(x, y)=\left\{ \begin{array}{ll} 1, &\text{ jika } x \neq y \\ 0, &\text{ jika } x=y. \end{array}\right.$

Metrik ini disebut metrik diskret.

Your Title Goes Here

Your content goes here. Edit or remove this text inline or in the module Content settings. You can also style every aspect of this content in the module Design settings and even apply custom CSS to this text in the module Advanced settings.

Mari Belajar Bersama Kami!