Ekuivalensi Definisi Limit Fungsi

Pada laman Definisi Limit Fungsi telah dijelaskan mengenai definisi limit fungsi dengan menggunakan $\epsilon$ dan $\delta$ . Akan tetapi, definisi ini kadang sulit untuk diterapkan dalam pembuktian. Seperti pada contoh dalam laman tersebut, pengambilan nilai $\delta$ agar aksioma definisi terpenuhi, sedikit tricky dan tidak mudah untuk mendapatkannya. Untuk itu, beberapa definisi lain yang ekuivalen dapat digunakan untuk membuktikan limit fungsi bilangan real ini.

Dalam pembahasan selanjutnya, diperlukan pemahaman lebih lanjut mengenai Barisan Bilangan Real.

Ekuivalensi Definisi Limit Fungsi

Diberikan $A\subseteq \mathbb{R}$ , $c$ titik kluster himpunan $A$ , dan $f:A\rightarrow\mathbb{R}$ . Tiga pernyataan berikut ekuivalen:

$\displaystyle{\lim_{x\rightarrow c}{f(x)}=L}$ .
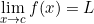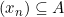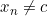Untuk setiap barisan $(x_{n})\subseteq A$ yang konvergen ke $c$ dan $x_{n}\neq c$ , untuk setiap bilangan asli 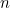$n$ , berakibat barisan 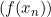$(f(x_{n}))$ konvergen ke $L$ .
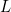Diberikan sebarang persekitaran 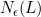$N_{\epsilon}(L)$ , terdapat persekitaran 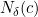$N_{\delta}(c)$ sehingga untuk setiap 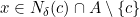$x\in N_{\delta}(c)\cap A \setminus \{c\}$ , berlaku $f(x)\in N_{\epsilon}(L)$ .

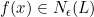Bukti. Akan ditunjukan ekuivalensi dari pernyataan-pernyataan berikut:

(1) $\Rightarrow$ (2)

Diambil sebarang barisan $(x_{n})\subset A$ yang konvergen ke $c$ dengan $x_{n}\neq c$ , untuk setiap bilangan asli $n$ . Akan ditunjukkan bahwa barisan $(f(x_{n}))$ konvergen ke $L$ . Diambil sebarang bilangan $\epsilon>0$ . Berdasarkan yang diketahui $\displaystyle{\lim_{x\rightarrow c}{f(x)}=L}$ , maka terdapat $\delta>0$ sehingga untuk setiap $x\in A$ dengan $0<|x-c|<\delta$ berlaku $|f(x)-L|<\epsilon$ . Lebih lanjut, dengan bilangan $\delta>0$ yang sama dan $(x_{n})\subset A$ yang konvergen ke $c$ dengan $x_{n}\neq c$ , untuk setiap bilangan asli $n$ maka terdapat bilangan asli $n_{0}$ sehingga $0<|x_{n}-c|<\delta$ , untuk setiap bilangan asli $n\geq n_{0}$ . Akibatnya, untuk setiap bilangan asli $n\geq n_{0}$ diperoleh

$\begin{equation*} |f(x_{n})-L|<\epsilon. \end{equation*}$

Jadi, untuk setiap bilangan $\epsilon>0$ , terdapat bilangan asli $n_{0}$ , sehingga untuk setiap bilangan asli $n\geq n_{0}$ , berlaku

$\begin{equation*} |f(x_{n})-L|<\epsilon. \end{equation*}$

Dengan kata lain, terbukti barisan $(f(x_{n}))$ konvergen ke $L$ .

(2) $\Rightarrow$ (3)

Untuk membuktikan pernyataan ini, akan digunakan pembuktian kontrapositif. Andaikan pernyataan (3) tidak benar. Dengan demikian, terdapat persekitaran $N_{\epsilon_{0}}(L)$ sehingga untuk setiap persekitaran $N_{\delta}(c)$ , terdapat paling sedikit satu $x_{0}\in A\cap N_{\delta}(c)$ dengan $x_{0}\neq c$ dengan sifat $f(x_{0})\notin N_{\epsilon_{0}}(L)$ . Jadi, untuk setiap bilangan asli $n$ , $N_{\frac{1}{n}}(c)$ memuat terdapat paling sedikit satu $x_{n}\in A\cap N_{\frac{1}{n}}(c)$ dengan $x_{n}\neq c$ dengan sifat $f(x_{n})\notin N_{\epsilon_{0}}(L)$ . Dengan demikian, diperoleh barisan $(x_{n})\subseteq A\cap N_{\frac{1}{n}}(c)$ dengan $x_{n}\neq c$ , untuk setiap bilangan asli $n$ dan $f(x_{0})\notin N_{\epsilon_{0}}(L)$ . Diperoleh $0<|x_{n}-c|<\frac{1}{n}$ dan $|f(x_{n})-L|\geq \epsilon_{0}$ . Dapat disimpulkan bahwa barisan $(x_{n})\subseteq A$ dengan $x_{n}\neq c$ , untuk setiap bilangan asli $n$ , konvergen ke $c$ , tetapi $(f(x_{n}))$ tidak konvergen ke $L$ . Terjadi kontradiksi dengan yang diketahui. Oleh karena itu pengandaian harus diingkarkan. Terbukti bahwa untuk setiap persekitaran $N_{\epsilon}(L)$ , terdapat persekitaran $N_{\delta}(c)$ sehingga untuk setiap $x\in N_{\delta}(c)\cap A \setminus \{c\}$ , berlaku $f(x)\in N_{\epsilon}(L)$ .

(3) $\Rightarrow$ (1)

Akan ditunjukkan $\lim_{x\rightarrow\infty}{f(x)}=L$ . Diambil sebarang bilangan $\epsilon>0$ . Berdasarkan yang diketahui, terdapat $\delta>0$ sehingga untuk setiap $x\in N_{\delta}(c)\cap A\setminus \{c\}$ berlaku $f(x)\in N_{\epsilon}(L)$ . Ekuivalen menyatakan, untuk setiap bilangan $\epsilon>0$ , terdapat $\delta>0$ , sehingga untuk setiap $x\in A$ , dengan $0<|x-c|<\delta$ , berlaku $|f(x)-L|<\epsilon$ .

Jadi, teorema terbukti.

$\blacksquare$

Mari Belajar Bersama Kami!

Ekuivalensi Definisi Limit Fungsi

Ekuivalensi Definisi Limit Fungsi

Mari Belajar Bersama Kami!

Submit a Comment Cancel reply