Latihan Ruang Metrik
Soal-soal berikut merupakan soal mengenai metrik. Untuk mengakses materi mengenai ruang metrik, silakan kunjungi laman berikut.
Soal
- Tunjukkan fungsi
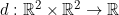 dengan
dengan
![Rendered by QuickLaTeX.com \[d(\bar{x},\bar{y})=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}\]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-be11c2e8a2e313c0c6fd0a19f4f53e92_l3.png)
untuk setiap
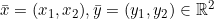 merupakan metrik pada
merupakan metrik pada 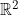 .
. - Jika
![Rendered by QuickLaTeX.com C[0,1]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-d662d16343173b856cd702565d81f6e0_l3.png) adalah himpunan semua fungsi kontinu dari
adalah himpunan semua fungsi kontinu dari ![Rendered by QuickLaTeX.com [0,1]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-3b003c79527e9e9639f54a1ad114bfe9_l3.png) ke
ke 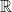 , tunjukkan fungsi
, tunjukkan fungsi ![Rendered by QuickLaTeX.com d_\infty: C[0,1]\times C[0,1] \rightarrow \mathbb{R}](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-9f24acdbbd169629002e96a657c7e40b_l3.png) denganJika
denganJika ![Rendered by QuickLaTeX.com C[0,1]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-d662d16343173b856cd702565d81f6e0_l3.png) adalah himpunan semua fungsi kontinu dari
adalah himpunan semua fungsi kontinu dari ![Rendered by QuickLaTeX.com [0,1]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-3b003c79527e9e9639f54a1ad114bfe9_l3.png) ke
ke 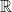 , tunjukkan fungsi
, tunjukkan fungsi ![Rendered by QuickLaTeX.com d_\infty: C[0,1]\times C[0,1] \rightarrow \mathbb{R}](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-9f24acdbbd169629002e96a657c7e40b_l3.png) dengan
dengan
![Rendered by QuickLaTeX.com \[d_\infty(f,g)=\sup\{|f(x)-g(x)|: x \in [0,1]\}, \text{ untuk setiap } f, g \in C[0,1]\]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-dff249c5ce5a88700d6fcb0ed1876b98_l3.png)
merupakan metrik pada
![Rendered by QuickLaTeX.com C[0,1]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-d662d16343173b856cd702565d81f6e0_l3.png) .
.
Jawaban:
Tinggal ditunjukkan fungsi ![]() memenuhi sifat definit positif, simetris, dan ketaksamaan segitiga.
memenuhi sifat definit positif, simetris, dan ketaksamaan segitiga.
(M2) Untuk setiap ![]()
![Rendered by QuickLaTeX.com \[\begin{array}{llll} d(\bar{x}, \bar{y})=0 &\Leftrightarrow& \sqrt{(x_1-y_1)^2+(x_2-y_2)^2}=0\\ & \Leftrightarrow&(x_1-y_1) =0 \text{ dan } (x_2-y_2)=0\\ &\Leftrightarrow& x_1= y_1 \text{ dan } x_2 =y_2. \end{array}\]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-ece7bba7cd6158f39a72fd1e8d0860b2_l3.png)
(M3) Untuk setiap ![]()
![Rendered by QuickLaTeX.com \[\begin{array}{ll} d(\bar{x}, \bar{y}) &= \sqrt{(x_1-y_1)^2+(x_2-y_2)^2}\\ & = \sqrt{(y_1-x_1)^2+(y_2-x_2)^2}\\ & = d(\bar{y}, \bar{x}). \end{array}\]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-3b77d891c1af428e70fccef8ef3cdc31_l3.png)
(M4)Untuk meunjukkan fungsi ![]() memenuhi sifat ketaksamaan segitiga, kita menggunakan Teorema ketaksamaan Minkowski.
memenuhi sifat ketaksamaan segitiga, kita menggunakan Teorema ketaksamaan Minkowski.
Teorema (Minkowski Teorema)
Jika ![]() maka
maka
![]()
Diambil ![]() ,
, ![]() ,
, ![]() dan
dan ![]() untuk
untuk ![]() maka
maka
![Rendered by QuickLaTeX.com \[\begin{array}{ll} d(\bar{x}, \bar{y}) & = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2}\\ & =(\displaystyle\sum_{i=1}^2 (x_i-y_i)^2)^{1/2}\\ & = (\displaystyle\sum_{i=1}^2 (((x_i-z_i)+(z_i-y_i))-((z_1-y_1))+(z_2-y_2))^2 )^{1/2}\\ & \leq \sqrt{(x_1-z_1)^2+(x_2-z_2)^2} + \sqrt{(z_1-y_1)^2+(z_2-y_2)^2}\\ & = d(\bar{x}, \bar{z}) +d(\bar{z},\bar{y}). \end{array} \]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-6898d4de54e1409a22993cf472c09384_l3.png)
Jadi terbukti ![]() metrik pada
metrik pada ![]()
2.Karena supremum dari nilai mutlak selalu positif maka untuk setiap ![]() berlaku
berlaku ![]() . Tinggal ditunjukkan fungsi
. Tinggal ditunjukkan fungsi ![]() memenuhi sifat definit positif, simetris, dan ketaksamaan segitiga.
memenuhi sifat definit positif, simetris, dan ketaksamaan segitiga.
(M2) Diambil sebarang ![]() , maka
, maka
![Rendered by QuickLaTeX.com \[\begin{array}{lll} d_\infty(f, g)=0 & \Leftrightarrow & \sup\{|f(x)-g(x)|: x \in [0,1]\} =0 \\ & \Leftrightarrow & |f(x)-g(x)|=0 \text{ untuk setiap } x \in [0,1].\\ & \Leftrightarrow & f(x) =g(x) \text{ untuk setiap } x \in [0,1].\end{array}\]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-a1219b09e44fac62b31a301f9f81fcbe_l3.png)
(M3) Diambil sebarang ![]() , maka
, maka
![Rendered by QuickLaTeX.com \[\begin{array}{lll} d_\infty(f, g) & = \sup\{|f(x)-g(x)|: x \in [0,1]\} \\ & =\sup\{|g(x)-f(x)|: x \in [0,1]\} \\ & = d_\infty(g, f). \end{array}\]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-1bac5f0634cc507f905495b83b69ba1f_l3.png)
(M4) Akan ditunjukkan ketaksamaan segitiga. Diambil sebarang ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{ll} d_\infty(\bar{x}, \bar{y}) & = \sup\{|f(x)-g(x)|: x \in [0,1]\}\\ & \leq \sup\{|f(x)-h(x)|+|h(x)-g(x)|: x \in [0,1]\}\\ & \leq\sup \{|f(x)-h(x)|: x \in [0,1]\}+ \sup \{|h(x)-g(x)|: x \in [0,1]\}\\ & = d_\infty(f, h)+d_\infty(h,g). \end{array} \]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-9b8647a8550db44b108955d4987e0efb_l3.png)
Jadi terbukti ![]() metrik pada
metrik pada ![]()
