Barisan Konvergen
Pada bagian ini akan dijelaskan tentang pengertian kekonvergenan barisan bilangan real. Suatu barisan dikatakan konvergen jika limit barisannya ada. Konsep limit barisan merupakan konsep dasar (basic) dalam matematika analisis. Kekonvergenan pada barisan bilangan real, selanjutnya bisa digeneralisasi pada ruang metrik atau ruang topologi. Untuk lebih jelasnya, berikut diberikan definisi limit barisan.

Definisi Limit Barisan
Diketahui ![]() barisan bilangan real. Suatu bilangan real
barisan bilangan real. Suatu bilangan real ![]() dikatakan limit (dari)
dikatakan limit (dari) ![]() jika untuk setiap
jika untuk setiap ![]() , terdapat
, terdapat ![]() sehingga untuk setiap
sehingga untuk setiap ![]() berlaku
berlaku ![]() .
.
Dalam hal ini ditulis
![]()
atau
![]()
Jika ![]() limit barisan
limit barisan ![]() , maka dikatakan
, maka dikatakan ![]() konvergen ke
konvergen ke ![]() atau
atau ![]() mempunyai limit
mempunyai limit ![]() .
.
Barisan yang mempunyai limit disebut barisan konvergen. Barisan yang tidak mempunyai limit dikatakan divergen.
Limit suatu barisan yang konvergen bernilai tunggal. Sifat ketunggalan limit barisan konvergen akan dijelaskan dalam Teorema berikut..
Teorema
Suatu barisan bilangan real yang konvergen mempunyai paling banyak satu limit barisan (tunggal).
Berikut pembuktian sifat ketunggalan limit barisan bilangan real yang konvergen.
Misalkan ![]() dan
dan ![]() .
.
Diambil sembarang ![]() Berarti ada
Berarti ada ![]() sedemikian sehingga
sedemikian sehingga ![]() dan
dan ![]() berlaku:
berlaku:
![]()
Diambil ![]() . Diperoleh
. Diperoleh ![]() berlaku
berlaku
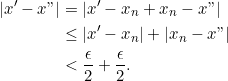
Karena ![]() sembarang, maka
sembarang, maka ![]()
Untuk lebih memahami definisi barisan konvergen, berikut diberikan contoh barisan konvergen beserta pembuktiannya.
Menggunakan definisi limit barisan, akan ditunjukkan bahwa barisan ![]() konvergen ke 0.
konvergen ke 0.
Berikut pembuktiannya.
Diambil sembarang ![]() . Berarti
. Berarti ![]() Menurut sifat Archimedes, ada
Menurut sifat Archimedes, ada ![]() sedemikian sehingga
sedemikian sehingga ![]() atau
atau ![]()
Jadi, untuk setiap ![]() berlaku
berlaku
![]()
Jadi, terbukti ![]() Dengan kata lain, terbukti
Dengan kata lain, terbukti ![]()
Menggunakan definisi limit barisan, dapat ditunjukkan juga kekonvergenan beberapa barisan berikut.
1. Barisan ![]() konvergen ke 0.
konvergen ke 0.
2. Barisan ![]() konvergen ke 2.
konvergen ke 2.
3. Barisan ![]() konvergen ke 0.
konvergen ke 0.
