Definisi Himpunan Terbuka dan Tertutup
Diketahui banyak sifat-sifat yang menarik berlaku pada interval ( contoh: fungsi kontinu bernilai real yang didefinisikan pada interval [a,b] akan mencapai maksimum dan minimumnya) dan ada beberapa jenis interval (interval terbuka, interval tertutup, interval setengah terbuka). Akan tetapi, banyak himpunan bagian dari himpunan semua bilangan real yang bukan merupakan interval.
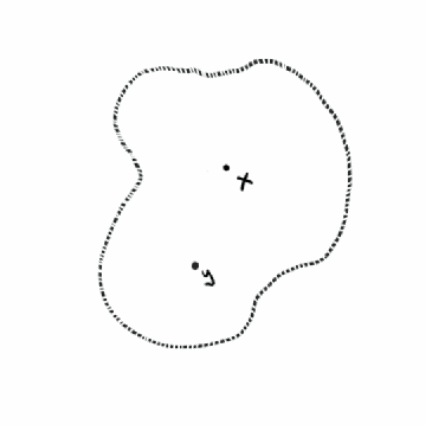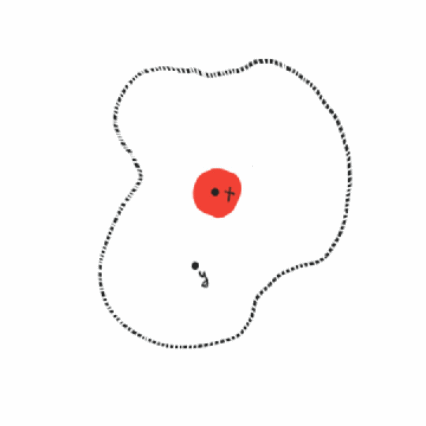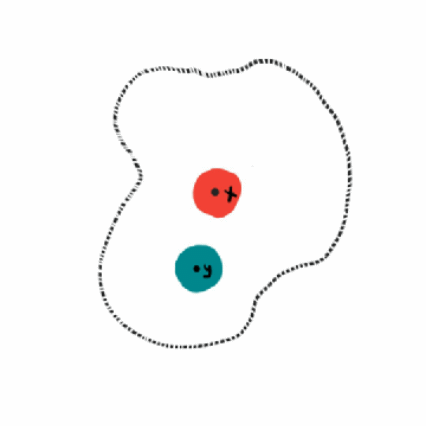
Oleh karena itu perlu pendefinisian himpunan terbuka dan himpunan tertutup pada ![]() secara umum. Ide pendefinisian himpunan terbuka diperoleh dari generalisasi interval terbuka dan untuk mendefinisikan himpunan terbuka dan tertutup diperlukan konsep persekitaran. Berikut diberikan definisi persekitaran di suatu titik
secara umum. Ide pendefinisian himpunan terbuka diperoleh dari generalisasi interval terbuka dan untuk mendefinisikan himpunan terbuka dan tertutup diperlukan konsep persekitaran. Berikut diberikan definisi persekitaran di suatu titik ![]() .
.
Definisi persekitaran
Diberikan titik ![]() dan
dan ![]() . Himpunan
. Himpunan ![]() disebut persekitaran dari
disebut persekitaran dari ![]() jika terdapat persekitaran-
jika terdapat persekitaran-![]()
![]() dari
dari ![]() sehingga
sehingga ![]()

Definisi himpunan terbuka dan himpunan tertutup
- Himpunan
 dikatakan terbuka di
dikatakan terbuka di 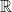 jika untuk setiap
jika untuk setiap 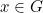 , terdapat persekitaran
, terdapat persekitaran 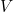 dari
dari  sehingga
sehingga 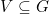 .
. - Himpunan
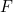 dikatakan tertutup di
dikatakan tertutup di 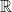 jika
jika 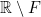 terbuka di
terbuka di 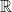 .
.
Karena untuk setiap persekitaran-![]()
![]() dari
dari ![]() berlaku
berlaku ![]() dan
dan ![]() terbuka (untuk bukti lihat di sini, maka
terbuka (untuk bukti lihat di sini, maka
| himpunan |
Seperti yang diketahui bahwa di dalam ruang lingkup topologi tidak menggunakan istilah “jarak”, maka untuk sebarang himpunan perlu diformulasikan kembali pengertian persekitaran dipandang dari sisi topologi. Definisi persekitaran diberikan berikut:
|
Diketahui \[x \in U \subseteq V.] |
Contoh
- Interval
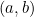 terbuka di
terbuka di 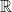 , untuk setiap
, untuk setiap 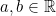 . Jelas, karena untuk setiap
. Jelas, karena untuk setiap 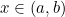 terdapat
terdapat 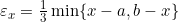 sehingga
sehingga 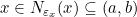 .
. - Himpunan kosong
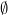 terbuka di
terbuka di 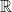 . Hal ini jelas karena himpunan kosong tidak memuat elemen sehingga memenuhi kondisi definisi himpunan terbuka.
. Hal ini jelas karena himpunan kosong tidak memuat elemen sehingga memenuhi kondisi definisi himpunan terbuka.
Himpunan semua bilangan real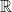 terbuka karena jelas untuk setiap
terbuka karena jelas untuk setiap 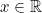 , dapat ditemukan
, dapat ditemukan 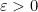 sehingga
sehingga 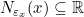 .\\
.\\
Karena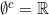 dan
dan 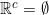 , maka himpunan
, maka himpunan 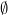 , dan
, dan 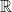 juga tertutup.
juga tertutup.