Definisi Himpunan Kompak
Diketahui bahwa setiap fungsi kontinu yang didefinisikan pada interval tertutup adalah fungsi yang kontinu seragam (untuk bukti dari sifat ini pembaca disarankan membaca artikel berikut). Peranan interval tertutup di sini dapat digantikan dengan sebarang himpunan kompak. Himpunan kompak merupakan salah satu konsep yang sangat penting di real analisis dan banyak perannya di aplikasi. Himpunan kompak di sini akan didefinisikan dengan liput terbuka.
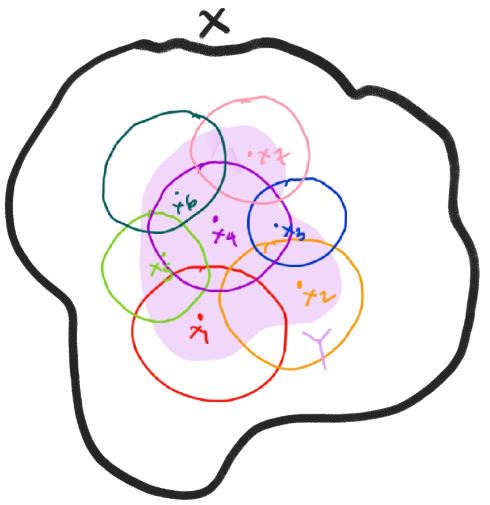
Definisi Liput Terbuka
Diberikan himpunan ![]() . Liput terbuka dari
. Liput terbuka dari ![]() adalah koleksi
adalah koleksi ![]() sehingga
sehingga
![]()
Jika ![]() subkoleksi dari
subkoleksi dari ![]() sehingga gabungan dari himpunan-himpunan di
sehingga gabungan dari himpunan-himpunan di ![]() juga memuat
juga memuat ![]() , maka
, maka ![]() disebut liput bagian dari
disebut liput bagian dari ![]() . Lebih lanjut, jika anggota himpunan-himpunan
. Lebih lanjut, jika anggota himpunan-himpunan ![]() berhingga maka
berhingga maka ![]() disebut liput bagian berhingga.
disebut liput bagian berhingga.
Suatu himpunan bagian di ![]() dapat memiliki banyak liput terbuka. Berikut beberapa contoh liput terbuka untuk
dapat memiliki banyak liput terbuka. Berikut beberapa contoh liput terbuka untuk ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{ll}\mathcal{G}_0 & = \{(-1, \infty)\},\\\mathcal{G}_1 & = \{(r-2, r+1): r \in \mathbb{Q}, r >0\},\\\mathcal{G}_2 & = \{(n-2, n+1): n \in \mathbb{N}\},\\\mathcal{G}_3 &=\{(-1,n): n \in \mathbb{N}\},\\\mathcal{G}_4 &=\{(-\frac{1}{n}, n): n \in \mathbb{N}, n \geq 20\}.\end{array}\]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-84c5931f0d817be7f1daea12a4ce15d6_l3.png)
Karena ![]() untuk setiap
untuk setiap ![]() dan
dan ![]() , maka
, maka ![]() merupakan liput bagian dari
merupakan liput bagian dari ![]() . Diberikan koleksi ,
. Diberikan koleksi ,![]() . Karena
. Karena ![]() maka
maka ![]() liput dari
liput dari ![]() . Karena
. Karena ![]() tidak terbuka untuk setiap
tidak terbuka untuk setiap ![]() maka
maka ![]() bukan liput terbuka
bukan liput terbuka ![]() .
.
Definisi Himpunan Kompak
DHimpunan ![]() dikatakan kompak jika untuk setiap liput terbuka dari
dikatakan kompak jika untuk setiap liput terbuka dari ![]() mempunyai liput bagian berhingga yang berhingga.
mempunyai liput bagian berhingga yang berhingga.
Dengan kata lain, untuk setiap liput terbuka ![]() dari
dari ![]() , terdapat
, terdapat ![]() sehingga
sehingga
![]()
Dari Definisi himpunan kompak di atas, himpunan ![]() dikatakan tidak kompak jika terdapat liput terbuka
dikatakan tidak kompak jika terdapat liput terbuka ![]() dari
dari ![]() tetapi gabungan berhingga dari himpunan-himpunan di
tetapi gabungan berhingga dari himpunan-himpunan di ![]() tidak memuat
tidak memuat ![]() .
.
Dari contoh-contoh liput terbuka di atas, himpunan ![]() tidak kompak karena
tidak kompak karena ![]() liput terbuka dari
liput terbuka dari ![]() akan tetapi untuk setiap
akan tetapi untuk setiap ![]() berlaku
berlaku ![]() .
.
Contoh:
Diketahui ![]() merupakan himpunan bagian berhingga dari
merupakan himpunan bagian berhingga dari ![]() . Diberikan sebarang liput terbuka
. Diberikan sebarang liput terbuka ![]() . Untuk setiap
. Untuk setiap ![]() berlaku
berlaku
![Rendered by QuickLaTeX.com \[\begin{array}{lll}x_1 \in &G_{\alpha_1}\\x_2 \in &G_{\alpha_2}\\\vdots &\vdots \\x_n \in & G_{\alpha_n}.\end{array}\]](https://analisisreal.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-2f85b45a48b8c6ac5d593fe13c675b4a_l3.png)
Akibatnya gabungan dari himpunan-himpunan di koleksi ![]() memuat
memuat ![]() . Jadi,
. Jadi, ![]() kompak.
kompak.
