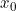TEORI APLIKASI TURUNAN
DEFINISI 1
Diberikan fungsi ![]() kontinu pada interval
kontinu pada interval ![]() dan
dan ![]() berada di
berada di ![]() . Titik
. Titik ![]() disebut titik kritis fungsi
disebut titik kritis fungsi ![]() jika
jika ![]() atau jika
atau jika ![]() tidak ada.
tidak ada.
DEFINISI 2
Fungsi ![]() mempunyai
mempunyai
- maksimum lokal di
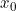 jika untuk setiap interval terbuka
jika untuk setiap interval terbuka 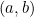 yang memuat
yang memuat 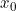 sehingga
sehingga 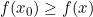 untuk setiap
untuk setiap 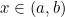 .
. - minimum lokal di
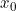 jika untuk setiap interval terbuka
jika untuk setiap interval terbuka 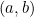 yang memuat
yang memuat 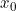 sehingga
sehingga 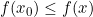 untuk setiap
untuk setiap 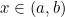 .
. - maksimum global di
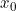 jika
jika 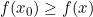 untuk setiap
untuk setiap  di domain
di domain 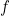 .
. - minimum global di
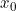 jika
jika 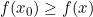 untuk setiap
untuk setiap  di domain
di domain 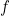 .
.
TEOREMA 3
Jika fungsi ![]() mempunyai maksimum lokal atau minimum lokal di
mempunyai maksimum lokal atau minimum lokal di ![]() , maka
, maka ![]() merupakan titik kritis fungsi
merupakan titik kritis fungsi ![]() .
.
BUKTI:
Diberikan fungsi ![]() mempunyai maksimum lokal atau minimum lokal di
mempunyai maksimum lokal atau minimum lokal di ![]() . Jika
. Jika ![]() tidak ada, maka menurut DEFINISI 1
tidak ada, maka menurut DEFINISI 1 ![]() merupakan titik kritis. Sebaliknya, jika diasumsikan bahwa fungsi
merupakan titik kritis. Sebaliknya, jika diasumsikan bahwa fungsi ![]() mempunyai maksimum lokal di
mempunyai maksimum lokal di ![]() dan
dan ![]() ada. Maka akan ditunjukkan bahwa
ada. Maka akan ditunjukkan bahwa ![]() .
.
Asumsikan bahwa ![]() , maka
, maka ![]() atau
atau ![]() . Jika
. Jika ![]() , maka jika untuk
, maka jika untuk ![]() cukup kecil, diperoleh
cukup kecil, diperoleh
![]()
dan ![]() tidak akan mempunyai maksimum lokal di
tidak akan mempunyai maksimum lokal di ![]() karena
karena ![]() . Analog, jika
. Analog, jika ![]() , maka untuk
, maka untuk ![]() cukup kecil, diperoleh
cukup kecil, diperoleh
![]()
dan ![]() tidak akan mempunyai maksimum lokal di
tidak akan mempunyai maksimum lokal di ![]() karena
karena ![]() . Akibatnya, diperoleh
. Akibatnya, diperoleh ![]() atau
atau ![]() merupakan titik kritis.
merupakan titik kritis.
Analog untuk ![]() mempunyai minimum lokal.
mempunyai minimum lokal.
TEOREMA 4
Diberikan fungsi ![]() diferensiabel di interval terbuka
diferensiabel di interval terbuka ![]() yang memuat
yang memuat ![]() . Maka
. Maka
- Jika
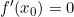 dan
dan 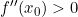 , maka
, maka 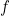 mempunyai minimum lokal di
mempunyai minimum lokal di 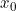
- Jika
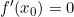 dan
dan 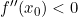 , maka
, maka 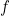 mempunyai maksimum lokal di
mempunyai maksimum lokal di