Nested Interval

Pada bagian ini akan dijelaskan tentang pengertian Nested Interval dan beberapa contohnya. Nested Interval Property merupakan salah satu sifat yang sangat berperan penting dalam pembuktian sifat tak terhitung (uncountabillity) himpunan bilang real. Sifat lengkap himpunan bilangan real yang sudah dijelaskan pada artikel Sifat Lengkap R memegang peran penting dalam hal pembuktian Nested Interval Property. Untuk lebih jelasnya, berikut diberikan terlebih dahulu definisi Nested Interval.

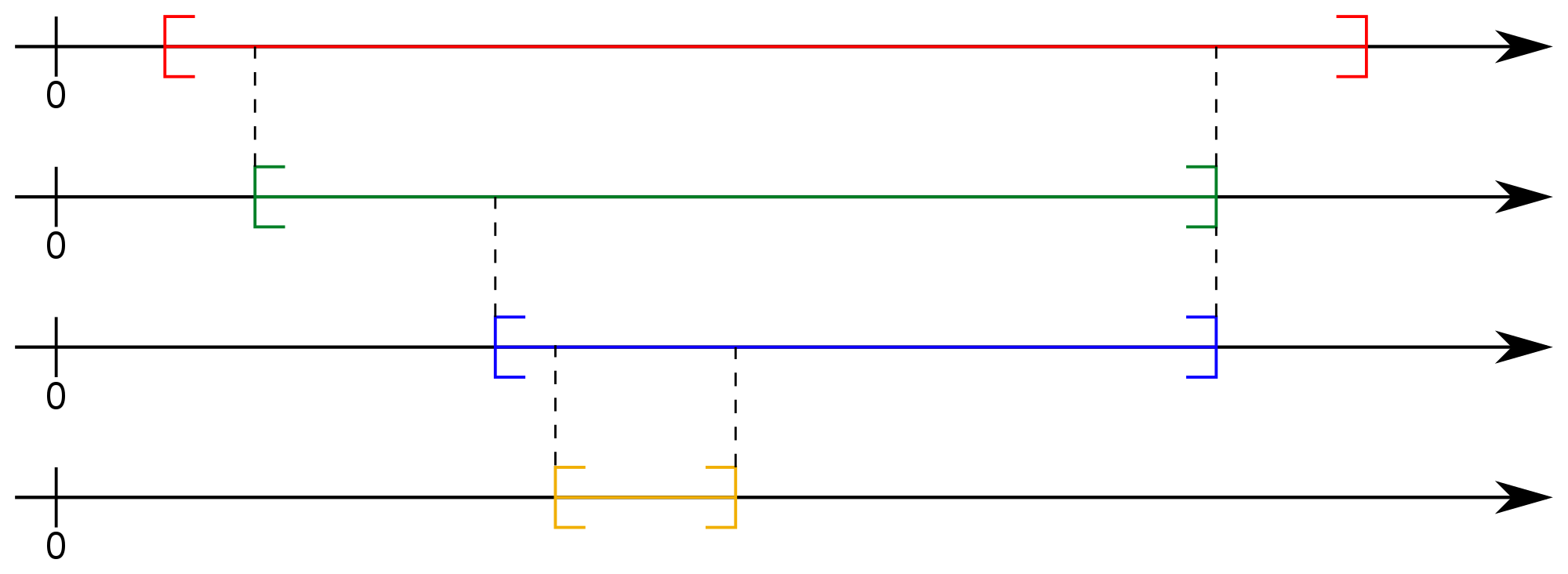
Definisi Nested Interval

Barisan interval $(I_n: n \in \mathbb{N})$ dikatakan Nested Interval jika

$I_1\supseteq I_2 \supseteq I_3\supseteq ...\supseteq I_n \supseteq I_{n+1}\supseteq...$

Agar lebih mudah dalam memahami definisi Nested Interval, berikut diberikan beberapa contohnya.

$I_n=[0,\frac {1}{n}], n \in \mathbb{N}$
$I_n=(0,\frac {1}{n}), n \in \mathbb{N}$
$I_n=[0,1+\frac {1}{n}], n \in \mathbb{N}$

Jika kita perhatikan dari beberapa contoh di atas, Nested interval belum tentu mempunyai elemen berserikat. Agar Nested interval mempunyai elemen berserikat dan tunggal, maka ada syarat cukup yang harus dipenuhi. Syarat cukup yang dimaksud akan dijelaskan dalam Nested Interval Property.

Nested Interval Property

Jika $I_n=[a_n,b_n], n\in \mathbb{N}$ interval tertutup terbatas dan $I_n\supseteq I_{n+1},\forall n\in \mathbb{N}$ , maka

$\cap_{n=1}^{\infty}I_n \neq\emptyset.$

(yaitu $\exists \mu \in \mathbb{R} \ni \mu \in I_n, \forall n \in \mathbb {N}$ )
Selanjutnya jika panjang $I_n=b_n-a_n$ memenuhi $\inf\{b_n-a_n|n \in \mathbb{N}\}=0,$ maka elemen berserikat $\mu$ tersebut tunggal.

Berikut pembuktian Nested Interval Property.

Namakan $A=\{a_n:n \in \mathbb{N}\}$ .
Jelas $A\neq\emptyset$ , $A\subset \mathbb{R}$ , dan $A$ terbatas ke atas
(sebab $I_1\supseteq I_n, \forall n \in \mathbb{N}$ sehingga $a_n \leq b_1, \forall n \in \mathbb{N}$ yang berarti $b_1$ batas atas $A$ ).
Menurut sifat lengkap $\mathbb{R}$ , maka $\sup A$ ada, yaitu terdapat $\alpha \in \mathbb {R}$ sedemikian sehingga $\alpha=\sup A.$
Jelas $a_m\leq\alpha, \forall m \in \mathbb{N}$ ……(*)
Untuk sebarang $m,n \in \mathbb{N}$ berlaku

$a_n\leq a_{m+n}\leq b_{m+n}\leq b_m$

atau

$a_n\leq b_m$

(berarti $b_m$ batas atas $\{a_n:n \in \mathbb{N}\}=A$ ). Akibatnya,

$\sup \{a_n:n \in \mathbb{N}\}\leq b_m$

atau $\alpha \leq b_m.$ ………(**)

Dari (*) dan (**) diperoleh

$a_m\leq\alpha\leq b_m,\forall m \in \mathbb{N}$

yang berarti

$\alpha \in I_m=[a_m,b_m],\forall m \in \mathbb{N}.$

Hal tersebut berakibat

$\cap_{m=1}^{\infty}I_m \neq\emptyset.$

Analog, jika $\beta=\inf \{b_n:n \in \mathbb{N}\}$ maka $\beta \in I_m, \forall m \in \mathbb{N}$ sehingga

$\beta \in \cap_{m=1}^{\infty}I_m .$

Jelas bahwa $\alpha \leq \beta.$

Selanjutnya akan dibuktikan ketunggalan dari elemen berserikat tersebut.

Diambil $\epsilon >0$ .
Karena $\inf \{b_n-a_n:n \in \mathbb{N}\}=0$ , maka terdapat $n_0 \in \mathbb{N}$ sedemikian sehingga

$0\leq \beta-\alpha\leq b_{n_0}-a_{n_0}<\epsilon$

atau

$0\leq \beta-\alpha <\epsilon.$

Karena $\epsilon >0$ sembarang, maka $\beta-\alpha=0$ atau $\beta=\alpha.$

Berdasarkan Nested Interval Property, Nested Interval mempunyai elemen berserikat jika intervalnya tertutup terbatas. Lebih lanjut, jika infimum dari himpunan panjang intervalnya bernilai nol, maka elemen berserikat dijamin tunggal.

Mari Belajar Bersama Kami!

Nested Interval

Definisi Nested Interval

Nested Interval Property

Mari Belajar Bersama Kami!

Submit a Comment Cancel reply