Persekitaran
Di dalam sistem bilangan real, nilai mutlak dari suatu bilangan real a diinterprestasikan sebagai jarak titik a ke titik asal 0. Dari interprestasi ini, diperoleh definisi umum dari jarak antara dua bilangan real a dan b yaitu nilai mutlak dari a-b. Istilah dekat biasanya berhubungan dengan jarak. Di matematika. Titik a dikatakan dekat dengan titik b jika jarak mereka a dan b “kecil“. Permasalahanya kapan jarak antara dua titik dikatakan kecil? Di dalam matematika, permasalahan ini dibahas dalam terminologi persekitaran.
Persekitaran merupakan salah satu konsep dasar yang sangat penting dan sering digunakan untuk memepelajari banyak konsep. Konsep persekitaran berhubungan dengan konsep himpunan terbuka dan interior. Definisi dari suatu titik interior dapat dilihat di “klik”, sedangkan untuk mendefinisikan persekitaran sendiri dibutuhkan pengertian persekitaran-![]() yang diberikan sebagai berikut
yang diberikan sebagai berikut
Definisi Persekitaran
Diberikan titik ![]() dan
dan ![]() . Persekitaran-
. Persekitaran-![]() dari
dari ![]() adalah himpunan
adalah himpunan ![]() .
.
Diperhatikan untuk setiap ![]() , pernyataan
, pernyataan ![]() berarti
berarti
![]()
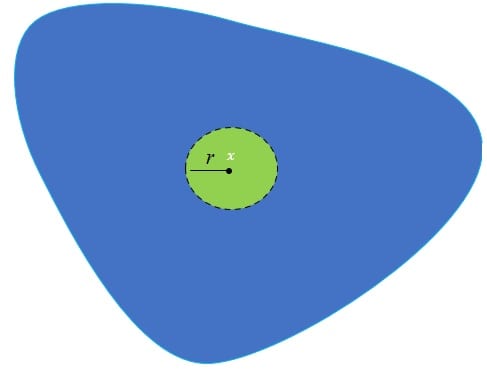
Berikut ini diberikan beberapa conto dari persekitaran-![]() .
.
- Diketahui
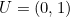 . Untuk setiap elemen di
. Untuk setiap elemen di  terdapat persekitaran-
terdapat persekitaran- yang termuat di
yang termuat di  . Untuk setiap
. Untuk setiap 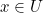 , diambil
, diambil 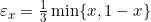 maka
maka 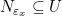 .
. - Diketahui
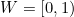 . Diberikan sebarang
. Diberikan sebarang 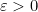 . Untuk setiap
. Untuk setiap 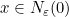 , terdapat
, terdapat 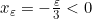 sehingga
sehingga 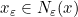 tetapi
tetapi 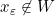 . Jadi, setiap persekitaran-
. Jadi, setiap persekitaran- dari 0 tidak termuat di
dari 0 tidak termuat di 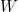 .
.
