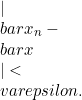Definisi Ruang Bernorma
Norma didefinisikan sebagai fungsi bernilai real yang di definisikan pada sebuah ruang vektor sebagaimana sehingga mempunyai sifat seperti jarak, yaitu tidak bernilai negatif, definite positif, homogenitas positif, dan berlaku ketaksamaan segitiga. Fungsi lain yang juga mempunyai sifat jarak adalah metrik. Selanjutnya, himpunan di mana norma tersebut didefinisikan disebut ruang bernorma.
Dengan norma atau fungsi jarak lainya, kita dapat mendefinisikan konsep-konsep dasar yang ada di analisis real seperti Kekonvergenan, Kekontinuan, dan Kekompakan.
Definisi Norma
Ruang bernorma adalah ruang vektor ![]() atas
atas ![]() ( atau
( atau ![]() ) yang dilengkapi fungsi \
) yang dilengkapi fungsi \
![]()
yang memenuhi sifat:
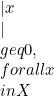 (non-negatif).
(non-negatif).-
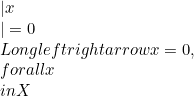 (definite positif).
(definite positif). 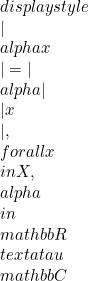 (homogenitas positif).
(homogenitas positif).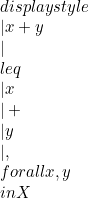 (ketidaksamaan segitiga).
(ketidaksamaan segitiga).
Selanjutnya, fungsi ![]() disebut norma pada
disebut norma pada ![]() .
.
Diberikan norma ![]() pada
pada ![]() . Didefinisikan fungsi
. Didefinisikan fungsi 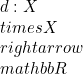 dengan
dengan 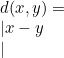 untuk setiap
untuk setiap ![]() . Jelas fungsi
. Jelas fungsi ![]() memenuhi sifat-sifat (1)-(4) pada metrik. Dari sini, kita menyimpulkan bahwa setiap ruang bernorma merupakan ruang metrik akan tetapi terdapat metrik yang bukan norma.
memenuhi sifat-sifat (1)-(4) pada metrik. Dari sini, kita menyimpulkan bahwa setiap ruang bernorma merupakan ruang metrik akan tetapi terdapat metrik yang bukan norma.
Contoh:
Diberikan ![]() . Diberikan metrik diskrit
. Diberikan metrik diskrit 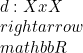 , yaitu
, yaitu
\
![]()
Jika ada norma ![]() sehingga
sehingga 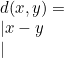 untuk setiap
untuk setiap ![]() , maka untuk
, maka untuk ![]() berlaku
berlaku 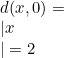 . Hal ini kontradiksi dengan
. Hal ini kontradiksi dengan ![]() . Jadi, metrik diskrit tidak dibangkitkan oleh sebuah norma.
. Jadi, metrik diskrit tidak dibangkitkan oleh sebuah norma.
Contoh:
Diberikan ![]() . Didefinisikan fungsi
. Didefinisikan fungsi 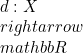 dengan \
dengan \
![]()
Menggunakan sifat nilai mutlak, sifat (1)-(4) dipenuhi. Norma ![]() dikenal dengan norma supremum. Jadi, ruang
dikenal dengan norma supremum. Jadi, ruang ![]() merupakan ruang bernorma.
merupakan ruang bernorma.
Ekuivalensi dua norma
Norma ![]() dan
dan ![]() pada ruang
pada ruang ![]() dikatakan ekuivalen jika terdapat dua bilangan real positif
dikatakan ekuivalen jika terdapat dua bilangan real positif ![]() sehingga \
sehingga \
![]()
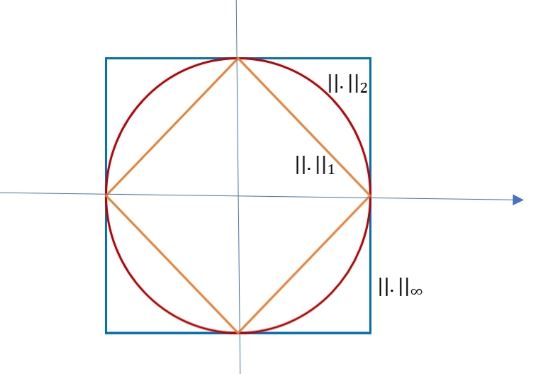
Contoh:
Norma ![]() dan
dan ![]() ekuivalen pada
ekuivalen pada ![]() .
.
Diketahui ![]() ruang bernorma dan
ruang bernorma dan ![]() . Persekitaran-
. Persekitaran-![]() dari
dari ![]() adalah himpunan
adalah himpunan
\
![]()
Berikut beberapa konsep di analisis real yang didefinisikan dalam ruang bernorma. Dengan mengganti persekitaran-![]() pada
pada ![]() dengan persekitaran-
dengan persekitaran-![]() pada ruang bernorma, sifat-sifat berkaitan yang ada di konvergen, kontinu dan topologi dapat dibuktikan juga berlaku di ruang bernorma
pada ruang bernorma, sifat-sifat berkaitan yang ada di konvergen, kontinu dan topologi dapat dibuktikan juga berlaku di ruang bernorma ![]() .
.
Diketahui ![]() ruang bernorma dengan norma
ruang bernorma dengan norma ![]() .
.
- Titik
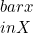 disebut titik limit himpunan
disebut titik limit himpunan 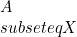 , jika untuk setiap persekitaran dari
, jika untuk setiap persekitaran dari 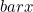 memuat paling sedikit satu titik
memuat paling sedikit satu titik 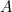 yang berbeda dengan
yang berbeda dengan 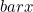 .
. - Fungsi
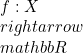 dikatakan kontinu di
dikatakan kontinu di 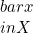 jika untuk setiap
jika untuk setiap 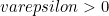 , terdapat
, terdapat 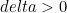 sehingga untuk setiap
sehingga untuk setiap 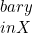 dengan
dengan 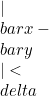 berlaku
berlaku 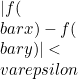 .
. - Titik
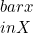 disebut limit barisan
disebut limit barisan 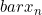 jika untuk setiap
jika untuk setiap 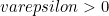 , terdapat
, terdapat 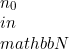 sehingga untuk setiap
sehingga untuk setiap 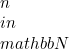 dengan
dengan 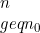 berlaku
berlaku